Does the Series Converge Absolutely Converge Conditionally or Diverge
The series diverges per the Integral Test because fx dx does not. -1 Choose the comect wawer below and if necessary in the answer box to complete your choice O A Theories converpes absolutely because the limit used in the nth-Tom Teet is OL The more converpes absolutely per the.

Does The Series Converge Absolutely Conditionally Or Diverge Sum 1 Math Methods Math Videos Cool Math Tricks
N 1 sin.

. N 2 sin. To say that an a n converges absolutely is to say that the terms of the series get small in absolute value quickly enough to guarantee that the series converges regardless of whether any of the terms cancel each other. Does the series X n1 1n n 1n2 converge absolutely converge conditionally or diverge.
So the series of absolute values diverges. Sum_ n1 inftysin n2sin frac 1 n2 Dachpunkt4cr 2022-02-25 Answered. Check the two conditions.
The series converges conditionally per the Alternating Series Test and because the limit used in the nth-Term Test is O C. The series converges absolutely because the limit used in the nth-Term Test is OE. Choose the correct answer below and if necessary fill in the answer box to complete your choice.
4 hours agoThe series converger conditionaty per the Question. Does the following series absolutely converge conditionally converge or diverge. Does the following series absolutely converge conditionally converge or diverge.
Kº 7 k1 diverges converges conditionally converges absolutely. -1 converge absolutely converge conditionally or does it diverge. The series converges conditionally per the Alternating Series Test and because the limit used in the Root Test is O B.
The Alternating Series Test will say that the series converges provided we can show that i lim n n 1n2 0 and ii the sequence of terms 1n2 are. 00 2 The series converges absolutely per the Comparison Test with E 3 n1 n OF. The series in the question converging means that S_n converges as a sequence.
You could make the denominator smaller by. Thus the alternating series a_k diverges. Conversely one could ask whether it is possible for to converge while diverges.
Hence our original series diverges. Solution for 1 Does the series converge absolutely converge conditionally or diverge. 4 Does the series 6 5 Prove that if the sequence a is convergent then it is bounded.
N2 converges the Limit Comparison Test says that the given series also converges. Use the Alternating Series Test to determine. Now let S_n be the partial series of the series in the question.
However we just found a subsequence that diverged. Since the series is alternating and not absolutely convergent we check for condi-tional convergence using the alternating series test with an 1 n23. Does the series - converge absolutely converge conditionally or diverge.
By definition a series converges conditionally when converges but diverges. The series converges absolutely because the limit used in the Root Test is O D. However in that case every subsequence of S_n converges.
The series converges absolutely since the corresponding series of absolute values is geometric with Ir O B. The series converges absolutely because the limit used in the Ratio Test is O D. Answer to 1 Does the series converge absolutely converge conditionally or diverge.
Does the series E- converge absolutely converge conditionally or diverge. For example n11n1 1 n2 n 1 1 n 1 1 n 2 converges absolutely. Ah but perhaps Ive said too much Hmm if you have only gotten to the comparison tests youd need to use a ratio bigger than the general term that you know will give a convergent series.
Absoluteconvergencesum_n1inftyfrac-1nn absoluteconvergencesum_n0inftyfracsinnn2 absoluteconvergencesum_n1inftyfraccosnn2 absoluteconvergencesum_n1infty-1nfracsinnn2. The following theorem shows that this is not possible. K1 Vk4 8 Oconverges absolutely converges conditionally diverges 1 1 VA 8 D SolutionInn.
The original series is not absolutely convergent. The series diverges because the limit used in the nth-Term Test does not exist. Also if you succeed in showing that this series converges absolutely since it contains no alternating term youll be done.
If an a n is conditionally convergent and r r is any real number then there is a rearrangement of an. The series converges conditionally because the corresponding series of absolute values is geometric with lr OB. Given the series an a n If an a n is absolutely convergent and its value is s s then any rearrangement of an a n will also have a value of s s.
If it does not converge then we say it does not converge absolutely and we move on to Step 2. The series diverges because the limit used in the Ratio Test is not less than or equal to 1. Further a n1 a because 1 n123 1 n23.
Lim n an lim n 1 n23 0. The series diverges because the limit used in the Ratio Test is not less than or equal to 1.

Does The Series Converge Absolutely Conditionally Or Diverge Sum 1 Math Methods Math Videos Cool Math Tricks
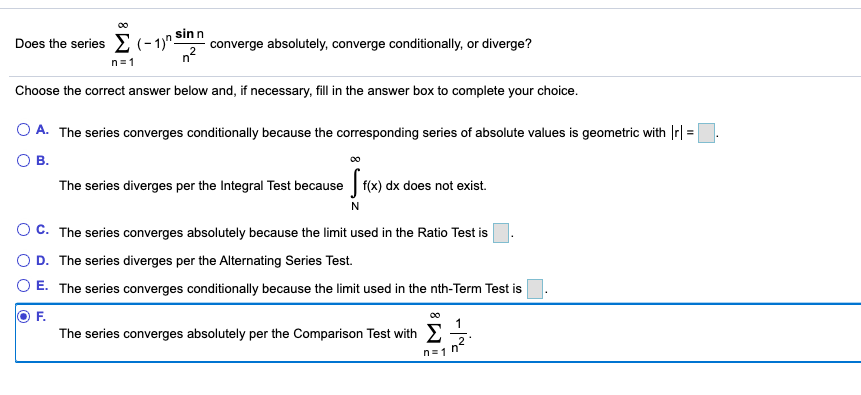
Solved Does The Series Converge Absolutely Converge Chegg Com
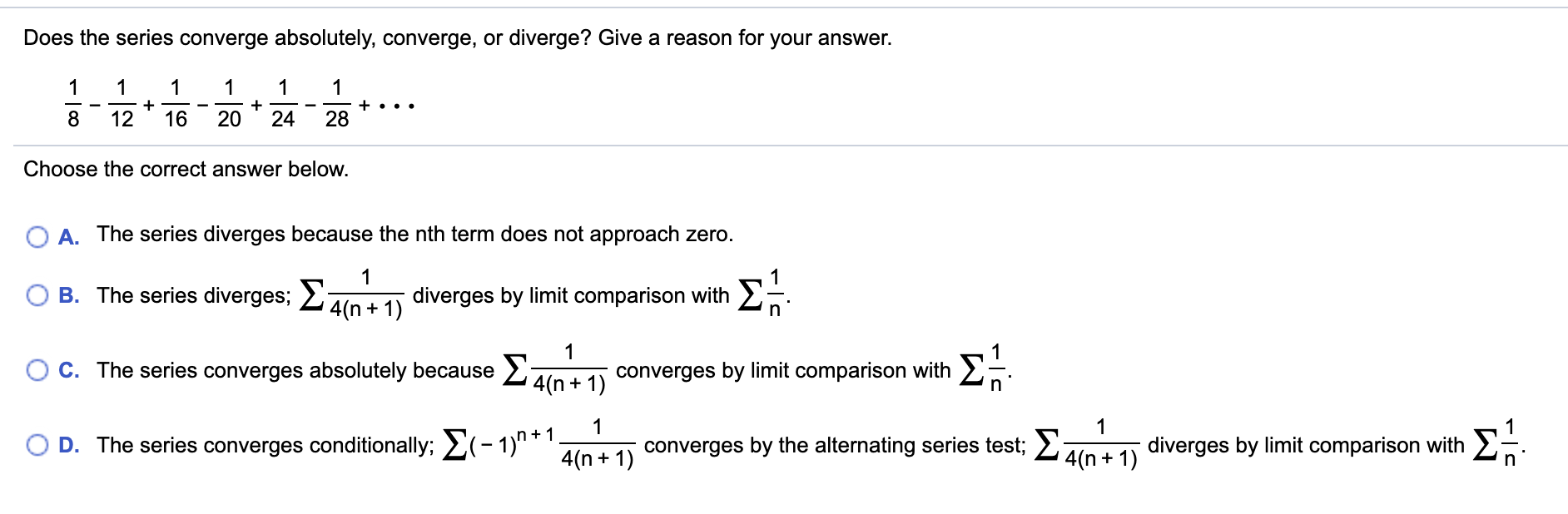
Solved Does The Series Converge Absolutely Converge Or Chegg Com
0 Response to "Does the Series Converge Absolutely Converge Conditionally or Diverge"
Post a Comment